Factors Affecting Bunker Silo Densities
by Brian J. Holmes1 and Richard E. Muck2
1Biological Systems Engineering Department, University of Wisconsin – Madison
2USDA, ARS, U.S. Dairy Forage Research Center
April 12th, 1999
Introduction
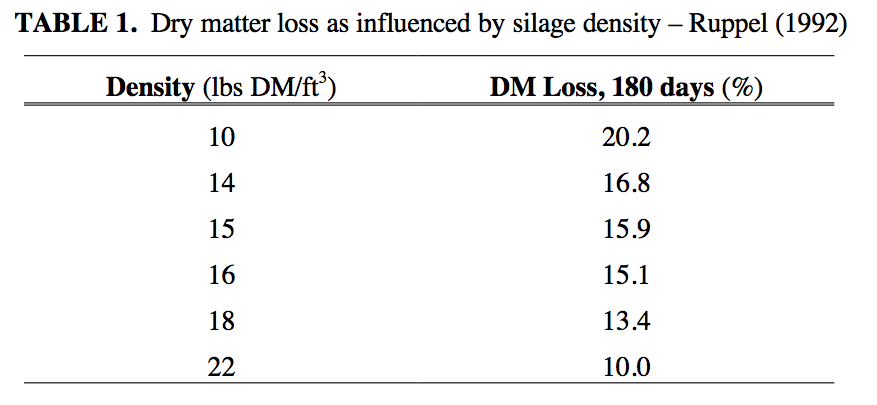
Attaining a high density in a silo is important for two primary reasons. Firstly and most importantly, density and dry matter content determine the porosity of the silage. Porosity, in turn, sets the rate at which air moves into the silo and subsequently the amount of spoilage which occurs during storage and feedout. Ruppel (1992) measured dry matter loss for alfalfa silage and developed an equation to relate the loss to density. Table 1 summarizes those results. Secondly, the higher the density, the greater the capacity of the silo. Thus, higher densities generally reduce the annual cost of storage per ton of crop by both increasing the amount of crop entering the silo and reducing crop losses during storage. The factors affecting density in bunker and pile silos are not well understood. General recommendations have been to spread the crop in 6-inch layers and pack continuously with heavy, single-wheeled tractors. In a survey of alfalfa silage in 25 bunker silos, Ruppel et al. (1995) found tractor weight and packing time (min/T As Fed or min/ft2) were the most important factors affecting density. However, both factors only explained a small fraction of the variation observed, and layer thickness was not measured. The objectives in our study were to measure density in a wider range of bunker silos and correlate those densities with filling practices.
Methods
Twenty collaborating county extension agents in Wisconsin measured densities in over 160 bunker silos containing either corn or haycrop (largely alfalfa) silage. Density was measured with a 2-inch diameter corer (Holmes, 1996), taking cores at approximately chest height at four locations across the silage face. Core depth, distance from the top and distance from the floor were recorded. Cores and a grab sample were mailed to the US Dairy Forage Research Center to determine weight, dry matter content, and particle size distribution. A survey was completed for each silo sampled. Information requested from farmers included: number of packing tractors, tractor weight, number of tires per tractor, tire pressure, tire condition, number of drive wheels, silage delivery rate, packing time per day, harvest time per day, filling time, filling technique, initial layer thickness, silo dimensions, maximum silage height, crop, crop maturity, and theoretical length of cut. These factors were then correlated with measured dry matter densities.
Results
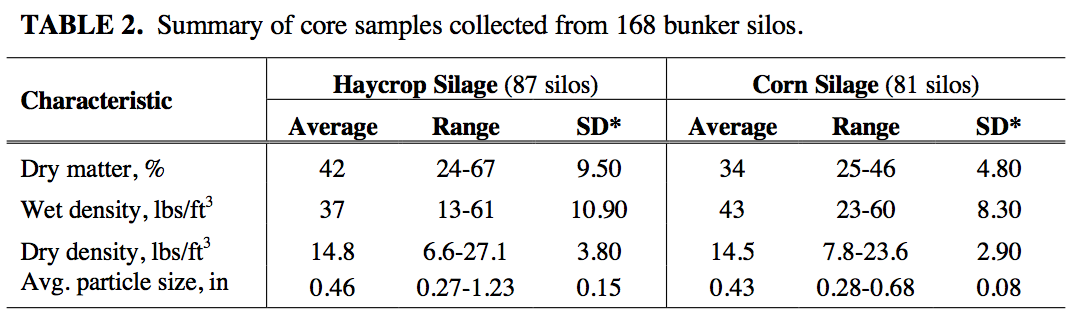
The range of densities and dry matter contents observed in haycrop and corn silages are shown in Table 2. Ranges of dry matter densities were similar for both haycrop and corn silages. Densities on the low end suggested little packing, whereas the highest densities were in the range observed in tower silos. Average dry matter densities were slightly higher than a recommended minimum density of 14 lbs DM/ft3.
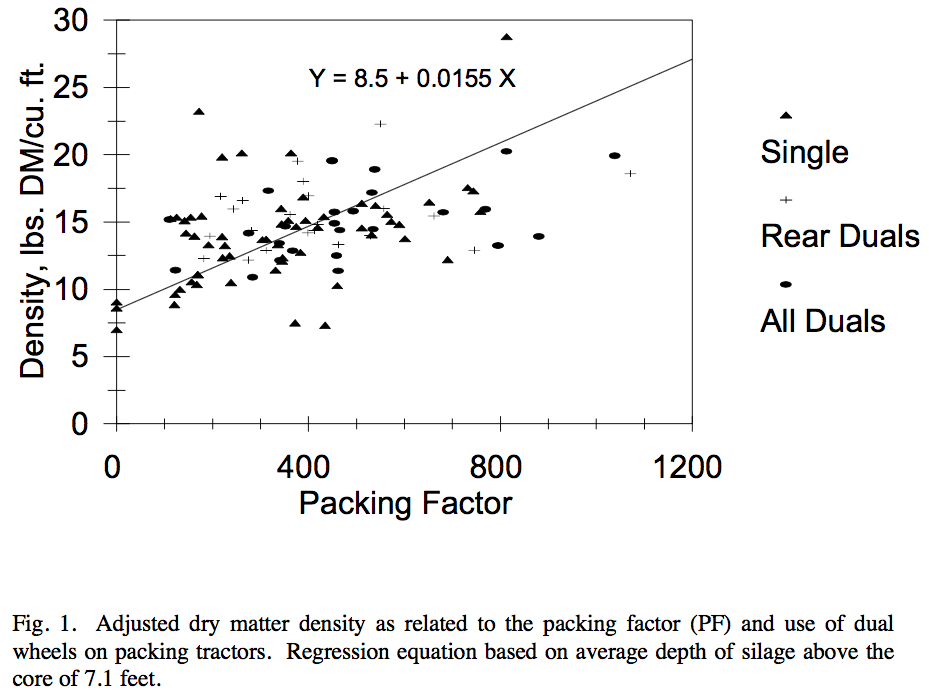
Densities were positively correlated with the height of silage above the core, indicating the effect of self-compaction in bunkers. To put densities on a common basis, all densities were adjusted to the median depth below the surface (7.1 ft) using Eq. 15 of Pitt (1983) and assuming a compressibility of 2.2 × 10-9/psi. Adjusted dry matter density was positively correlated with average packing tractor weight, packing time, and dry matter content. Density was inversely correlated with the initial depth of the crop layer when spread in the silo.
The linear regression which explains 18% of the variation (Fig. 1) of estimated dry matter density (DMD) is expressed as:
Est. DMD (lbs DM/ft3) = (8.5 + PF × 0.0155) × (0.818 + 0.0136 × D) [1]
where average depth (D) and packing factor (PF) are calculated as:
D = average silage depth (ft) = (height at wall + height at center) ÷ 2
PF = (W ÷ L) × √(N × DM ÷ C) [2]
W = Proportioned average tractor weight (lbs) for all tractors packing silage. Example: Two tractors pack 100% of the filling time; tractor #1 weighs 25,000 lbs and tractor #2 weighs 15,000 lbs. Then the proportioned average tractor weight is 20,000 lbs = (25,000 + 15,000) ÷ 2. If tractor #1 packs 90% of filling time and tractor #2 is used 50% of the time, the proportioned average tractor weight becomes:
19,286 lbs = (25,000 × 0.9 + 15,000 × 0.5) × [90 ÷ (90 +50)]
L = Layer thickness (inches) of the spread but unpacked crop in the silo prior to driving over it during the first packing pass.
N = Number of tractor-packing equivalents, where N = 1 when one tractor is packing continuously during the filling process. This value can be fractional, reflecting one or more tractors packing intermittently. For example, if one tractor packs continuously during the silo-filling process and another packs 50% of the filling time, N = 1 + 0.5 = 1.5. If there is only one packing tractor and it packs for 11 hr/day and the silo is filled 10 hr/day, then N = 11/10 = 1.1.
DM = Dry matter content (decimal).
For example, 35% dry matter forage is used as 0.35 in the equation.
C = Crop delivery rate (T AF/hr) to the silo.
Use of rear duals or all duals on packing tractors, as shown in Fig. 1, had little effect on density. Other factors such as tire pressure, crop, and average particle size were not significantly correlated with density. Thus the low r2 of the regression of dry matter density vs. the 5-parameter packing factor probably reflects variability in accurately estimating parameters such as initial depth of the crop and packing time per ton rather than missing factors important to determining density.
One practical issue raised in the study was packing time relative to crop delivery rate to the silo. Packing time per ton was highest (1 to 4 min/T As Fed) under low delivery rates (<30 T As Fed/h) and generally declined with increasing delivery rate. Packing times were consistently less than 1 min/T As Fed at delivery rates above 60 T/h in our survey. These results suggest that farmers using contractors to harvest their silage crops probably will need to pay particular attention to spreading the crop in a thin layer and would benefit from using several packing tractors simultaneously.
Let’s consider the example of filling a bunker silo which is 40 feet wide, has 10-foot sidewalls, and is packed to a maximum depth of 14 feet at the center. The 35% dry matter content silage is delivered to the silo at the rate of 100 T AF per hour. One packing tractor (25,000 lbs) distributes silage with a blade to a depth of 12 inches per layer and packs continuously when not pushing up silage. A second tractor (15,000 lbs) packs continuously. Assuming a triangular-shaped cross section above the 10-foot walls, the average silage depth is:
D = (10 ft + 14 ft) ÷ 2 = 12 ft.
The average packing tractor weight is:
W = (25,000 lbs + 15,000 lbs) ÷ 2 = 20,000 lbs.
The packing layer thickness is:
L = 12 inches.
The crop delivery rate is:
C = 100 T AF/hr.
The dry matter content of the silage is:
DM = 0.35
Using these values, the packing factor can be calculated as:
PF = (20,000 lbs ÷ 12 in) × √(2 tractors × 0.35 ÷ 100 T AF/hr)
PF = 1667 × 0.084 = 140.
Using Equation 1, the expected dry matter density is:
DMD = (8.5 + 0.0155 × 140) × (0.818 + 0.0136 × 12) = 10.5 lbs DM/ft3
Being less than 14 lbs DM/ft3, a change in packing procedure would be beneficial.
The following options for improving compaction are suggested. The are in order of increasing cost of difficulty of implementation.
Decrease packing layer thickness from 12 inches to 6 inches.
PF = (20,000 lbs ÷ 6 inches) × 0.084 = 280.
Using Equation 1, the expected dry matter density becomes:
DMD = (8.5 + 0.0155 × 280) × (0.818 + 0.0136 × 12) = 12.6 lbs DM/ft3.
Since this dry matter density is less than 14 lbs DM/ft3, consider adding weight to the tractors. This can be done by adding fluid to the tires, adding front end weights, adding steel wheel weights, adding a concrete block on the 3-point hitch, or adding dual wheels with fluid and/or wheel weights. Let’s assume 6,000 lbs can be added to each tractor. The average tractor weight then becomes:
W = (31,000 lbs + 21,000) ÷ 2 = 26,000 lbs.
Assuming the same 6-inch packing layer thickness, the packing factor then increases to:
PF = 26,000 ÷ 6 × 0.084 = 364.
With these conditions, the expected dry matter density is:
DMD = (8.5 + 0.0155 × 364) × (0.818 + 0.0136 × 12) = 13.9 lbs DM/ft3
…which is close to the minimum 14 lbs DM/ft3. Other methods for increasing the packing factor and thus the dry matter density are:
- Reduce delivery rate of silage to the bunker this increasing the packing time per ton.
- Increase dry matter content by allowing longer crop field drying time.
- Increase depth of silage in the bunker silo.
- Increase average tractor weight by adding more weight to each tractor, or replace existing tractors with heavier tractors.
- Add more packing tractors. Use heavier rather than lighter tractors so the average weight is not reduced when adding a tractor.
- Reduce packing layer thickness further.
- Pack for additional time.
Items a. to c. are somewhat difficult to accomplish if the harvest rate and bunker silo are currently being pushed to the limit. Few will be willing to slow the harvest rate so packing can be accomplished. Fermentation occurs best in the range of 30-40% dry matter. Increasing dry matter content beyond 40% to improve density is counterproductive for good fermentation. If the bunker is full, adding silage depth above the full mark can be dangerous.
Items d. to g. are more often within the control of the producer. Producers achieving high packing density have adopted the use of very heavy tractors and are using a shallow (< 6-inch) packing layer thickness. When the delivery rate to the silo is quite high (as with self-propelled harvesters operating in corn silage), one or more additional packing tractors are added. In a well-packed silo, tractor tires will pass over the entire packing layer surface at least once.
An Excel spreadsheet has been developed to make the calculation procedure easier. Download the spreadsheet by clicking the link below:
Bunker Silo Density Calculator
A procedure for estimating the density of silage in a bunker silo based on silage packing has been described. Silage of high density experiences less dry matter loss than does that of lower density. Table 1 can be used to estimate the savings in dry matter by increasing the silagemdensity. For example, increasing the density from 14 lbs DM/ft3 to 16 lbs DM/ft3, the expected dry matter savings is approximately 1.7% (16.8%-15.1%). If silage is worth $85 TDM, the 1.7% reduced loss represents $1.45/TDM. Producers can use the procedure for estimating silage density to determine how much additional effort (cost) is needed to achieve an improved density. If the savings are more than the cost of achieving the savings, then it is economically viable to implement the changes needed to achieve the savings.
References
Holmes, B.J.. 1996. Probe for silage profit. Minnesota/Wisconsin Engineering Notes Newsletter, Fall.
Pitt, R.E. 1983. Mathematical prediction of density and temperature of ensiled forage. Trans. ASAE 26:1522-1527,1532.
Ruppel, K.A. 1992. Effect of bunker silo management on hay crop nutrient management. M.S. Thesis, Cornell University, Ithaca, NY.
Ruppel, K.A., R.E. Pitt, L.E. Chase, and D.M. Galton. 1995. Bunker silo management and its relationship to forage preservation on dairy farms. J. Dairy Sci.. 78:141-153.